The Carbohydrate Intrinsic (CHI) Energy Functions were developed to score oligosaccharide structures based on glycosidic linkage conformations. Quantum mechanical calculations were used to obtain the torsional energy profiles of glycosidic torsion angles using several tetrahydropyran-based disaccharide models. Similar energy profiles were grouped, and an average energy curve for each group was calculated, resulting in final four CHI energy equations described below. Currently, CHI energy functions can be applied to all standard two-bond glycosidic linkages between pyranoses in the chair conformation.
Equations
Summary tables of the equations are given below this section.
- CHI energy equation for the
torsion angle of disaccharides in which the C1O1 bond of the non-reducing saccharide is in the axial position:

where, -180 << 180
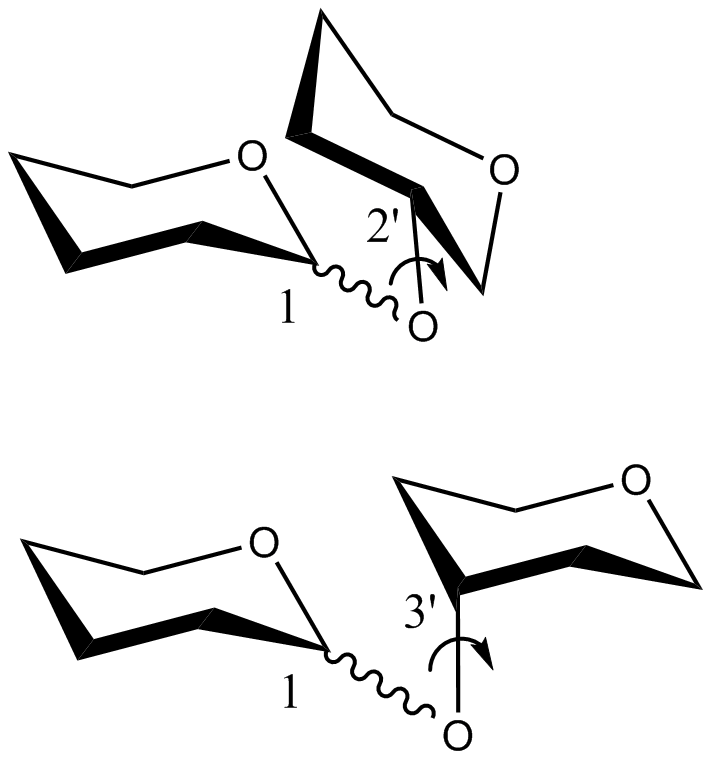
- CHI energy equation for the
torsion angle of disaccharides in which the C1O1 bond of the non-reducing saccharide is in the equatorial position:
where, -180 << 180
- CHI energy equation for the
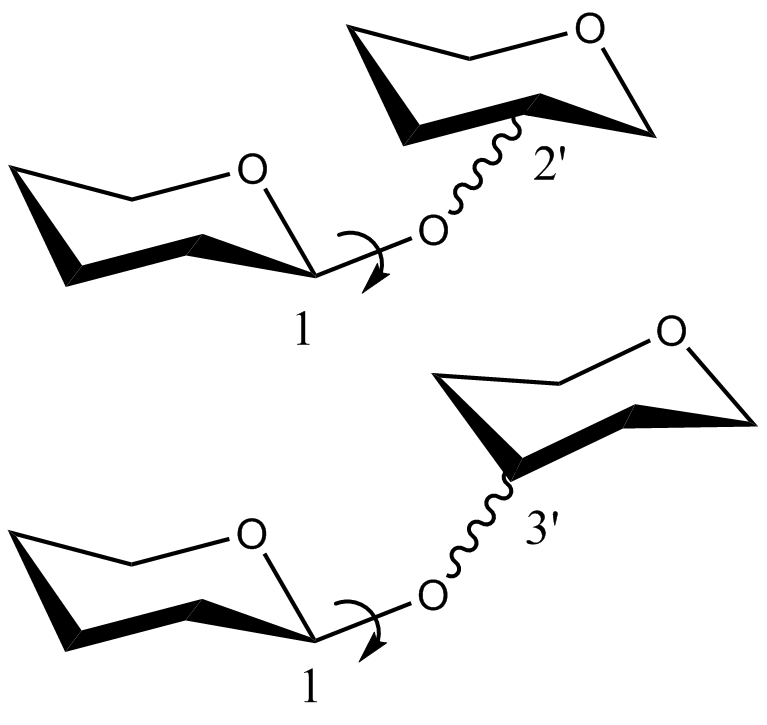
torsion angle of disaccharides in which the C2‘O2‘/C4‘O4‘ bond of the reducing saccharide is in the axial position or the C3O3 bond of the same saccharide is in the equatorial position:
where, 0 << 360
- CHI energy equation for the
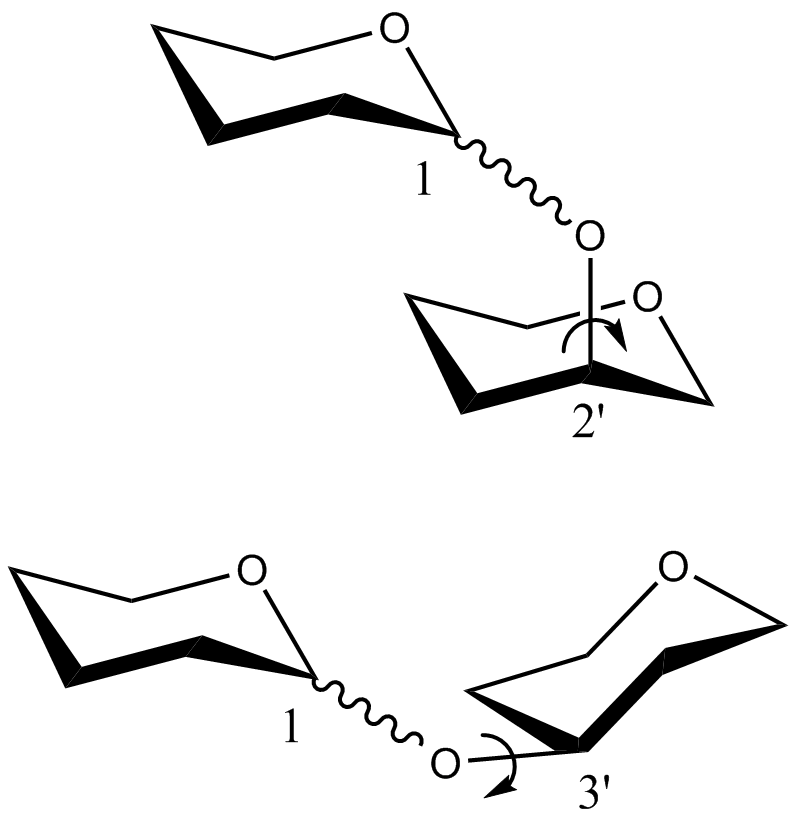
torsion angle for disaccharides in which the C2‘O2‘/C4‘O4‘ bond of the reducing saccharide is in the equatorial position or the C3O3 bond of the same saccharide is in the axial position:
where, 0 << 360
Summary of Equations
The CHI energy equations are of the generalized form:
The parameters for each of the four equations are given in the following tables:
Usage
In order to obtain the total CHI energy for a given oligosaccharide conformation, the CHI energies of the individual glycosidic torsion angles comprising the molecule are first calculated by substituting the corresponding torsion angle values in the appropriate CHI energy equations. The summation of the individual CHI energies gives the total CHI energy of the molecule.
Publication
A. K. Nivedha, S. Makeneni, B. L. Foley, M. B. Tessier , R. J. Woods, J. Comput. Chem. 2014, 35, 526–539. DOI: 10.1002/jcc.23517